The goal of K'dokū is to fill in each group of 12 numbers with one of each number (0-9,A,B). To do this, click on a cell. This will highlight all numbers in the same groups as the cell you clicked on. Then, fill in the cell with the number which does not occur anywhere else in the highlighted regions. There may be more than one number missing; in this case, try other spots and fill those in until the original cell can be determined.
To keep track of the numbers which could go in a single spot, you can select 'Notes' mode and enter a list of numbers. To remove a number, simply type it again.
Geometrically, a K'dokū works similarly to a Sudoku, except it uses the numbers 0-11 (0-9,A,B), and it uses four dimensions, not two. The K'dokū grid is made up of a 4×4×3×3 hyperrectangle, split into nine 4×4 squares. This creates two different types of 12-number spaces:
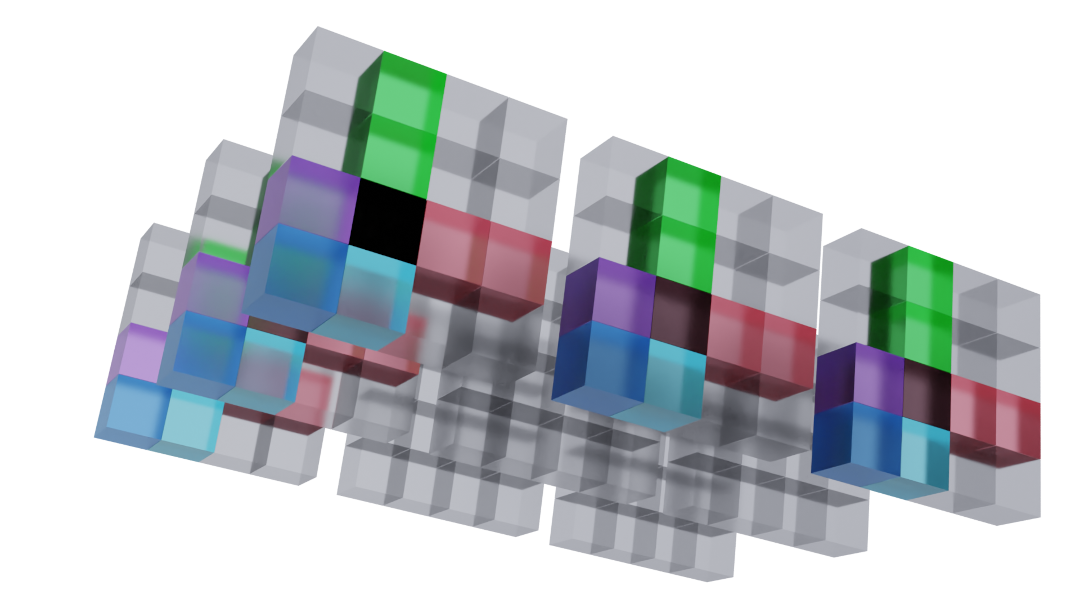
- A 3×4 plane with four orientations: xz, xw, yz, and yw (red, green)
- A 2×2×3 block with two orientations: xyz, xyw (blue)
Each of these regions must be filled with exactly one of each number, from 0-B. The goal of the K'dokū is to find which numbers must be in which locations to make a complete grid. Clicking on a cell above will highlight all cells in neighboring planes or blocks. These cells all must have a different value than the selected one for the puzzle to be solved.
If this sounds needlessly complicated, it should. This was created because of a joke, where I said I was going to make someone solve a 4D, base-12 sudoku. After I realized that it could actually exist, I had to make it.